 |
Web www.pumpfundamentals.com |
 |
Web www.pumpfundamentals.com |
MICRO-HYDRO INSTALLATION SIZING (PELTON AND TURGO WHEEL TURBINES)
A friend of mine asked me to help size a micro-hydro installation that he was thinking of installing at his cottage. Specifically he wanted to know how to calculate the flow rate of water through a pipe with a given vertical drop. This is a simple pump-sizing problem without a pump, so I thought I would give him a hand. It turned out to be a very interesting topic and I hope you will find it helpful in understanding the concept.
A micro turbine is a wonderful way to generate you own electricity because it is so ecologically friendly. It has little or no impact on the environment and will provide continuous energy year round at low cost. Unfortunately, not many of us can access this resource since it usually requires a large track of land with a stream. For those of us who live in the country, it is possible that you could have a stream nearby on public land that you could access. In this case it may require a longer line (or penstock) to get the water from its source to your land where you will put your micro-turbine. This article is about how you can figure out how much energy will be available considering your terrain and water availability.
This link will provide you with a pdf version![]() of this web page.
of this web page.

What is HEAD and why is it used?
The difference in height between the water source and the turbine location is the key to generating power. This height is known as head or more precisely static head. Head is expressed in feet just like height; the difference is when we use the term head, we are actually talking about energy per pound of liquid displaced. So head is just another term for energy, specifically energy per unit weight of liquid displaced. How is this possible? Energy, or useful work can be expressed as pound-feet or lbf-ft in the Imperial system. If I divide this term by lbf, I obtain lbf-ft/lbf or feet (ft) and this is what is known as head.

If I know how many pounds of liquid are displaced per unit time (this is proportional to flow rate in gallons per minute for example) then I know how much power is required since by multiplying head in lbf-ft/lbf by lbf/min, I get a unit of power in lbf-ft/min or foot-pounds per minute.

We know there are 550 lbf-ft/s in a horsepower and 1.34 horsepower in a kilowatt. Therefore, when we know the height difference, or static head, we can immediately get a good idea of how much energy will be available however the analysis is not complete without the flow rate.
Typical micro-hydro installation
The following image shows a typical system that I have seen and which I am familiar with. The stream is located on a hill or incline. The riverbed is accessible and you require some sort of structure that will hold your intake pipe held securely. Remember that heavy rains bring, high water levels and lots of activity within the stream, including the movement of large boulders that could disrupt, or destroy your intake if it is not built robustly enough.
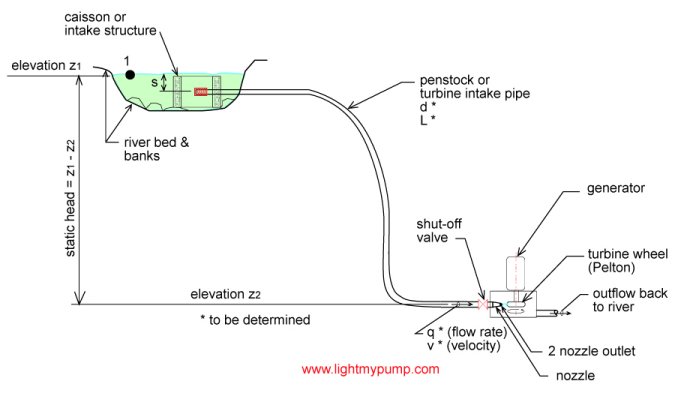
Intake design
The intake structure shown could also be called a caisson and it is built of re-enforced concrete approximately 3 feet by 3 feet by 2.5 feet high with 6-inch walls. It is basically a thick frame with 4 concrete walls. This is robust enough to stay put in the stream even when the heavy waters come and provides a stable structure to which you can attach your intake pipe. You should provide some sort of filtration device at your pipe intake to prevent branches and other detritus from entering the pipe. A heavy screen mesh is suitable and if you provide holes on the side of the pipe there will be more area for the water to enter the pipe, which causes less pressure drop.
Your pipe intake should be sufficiently submerged to prevent a vortex forming at the surface that would allow air to enter the pipe and reduce the flow. The height required to avoid vortex formation depends on the size of the pipe and the flow rate, which has yet to be determined. For those of you who would like to calculate the submergence height see this web app: https://www.pumpfundamentals.com/web-apps-1.htm. Typically for the flow rates that concern us an intake pipe end submergence of 2 feet is sufficient. Also you have to consider that the water level in the stream will vary throughout the year.
It's important that the intake pipe be smoothly laid out from start to finish avoiding upward runs as much as possible. It may be impossible to avoid this but keep vertical excursions as small as possible. In particular near the intake you must avoid going above the water level prior to going downwards to the turbine. This is to avoid the possibility of getting an air lock (i.e. trapped air in the intake pipe) that could prevent water reaching the turbine.
If you are in the northern latitudes you will have to consider what to do about freezing temperatures. Small streams on a sharp incline flow throughout the year no matter the temperature. If you keep flow running through your line, you will experience the same effect, and will not get a frozen and possibly damaged line. This is something you should consider in your set up. The alternatives are to bury the line or use heat tracing both of which are expensive and time consuming.

Let's get right to it and figure out what size pipe is suitable for our stream, what flow rate we can expect and how much power can be generated?
Intake pipe size
The intake pipe is the key to the whole installation and it will determine how much power can be generated. The other critical factor is the height or static head available between the surface of the stream and your turbine location. If the head is small, say 1 to 5 ft, then the amount of energy available will be very small and not worth the trouble.
The other consideration is how much water is in the stream, and how much can you take without building a major infrastructure at the intake. This can be hard to evaluate, and sometimes you just have to take a stab at it, and use this as a basis for calculating your power availability. You can then determine how this impacts the size of your intake structure, versus the size of the streambed.
All streams are different and the shape of the streambed varies considerably from one location to another. However, as a guideline use this table as a starting point for sizing your intake pipe.
| Stream width (ft) | Stream depth (ft) | Pipe dia. (in) |
| 4 | 1 | 1/2 - 3/4 |
| 12 | 4 | 3 - 4 |
Here's an example based on a 3 in pipe intake; the length of the pipe will be 100 ft, the static head is 10 ft. Once you have been through this you will be able to change these numbers and adapt them to your situation.
The first thing to do is determine the flow rate through the pipe knowing the pipe length and static head.
From the flow rate q, we can determine the velocity in the pipe with this equation:
Note: the units are indicated for each term within the equation. For those of you who wish to know how this equation is derived, see this web page: https://www.pumpfundamentals.com/micro-hydro_formulas.htm
The velocity in the pipe is related to the friction loss in the system and the energy (static head) that is available to drive the water from the upper stream bed to the turbine (those of you who want to know the origin of this formula, go to this link: https://www.pumpfundamentals.com/micro-hydro_formulas.htm
The units for all of these terms are feet. The term v2/2g works out to feet if you use ft/s as the velocity unit and ft/s2 for g.
z1 -z2 is the head and equals 10 ft, and v2 is the outlet velocity of the pipe at point 2 which we want to determine, and g is the acceleration due to gravity 32.17 ft/s2. HF is the friction loss in the pipe and depends on the velocity.
We would like to solve this equation for v2 by transferring the term HF to the other side like this:
and then taking the square root to find v2.
The problem is that HF depends on the velocity in the pipe, which depends on the flow rate. v2 also depends on the flow rate, so that we have to do an iteration to solve this equation. An iteration in this case means that we must suppose a value for the flow rate q, calculate v2 using equation (1) , calculate HF using one of several methods, then put this value back into equation (2) and see if we get the same value of v2. If not, we make a small modification to q and try again; it will likely take about 3 to 4 trials (or iterations) to get a fairly accurate value for v2.
The term HF is the friction in the system between points 1 and 2 or between the water level and the nozzle outlet. This includes:
- intake filter loss (negligible);
- fittings including valve loss (negligible);
- pipe length loss (to be determined); = HF
- nozzle loss;
The intake filter friction loss depends on the mesh size, the open area, etc. If we make a very tight screen we will have a high pressure drop and therefore high friction loss. It is possible to build an acceptable filter with a low friction loss, say 1 ft or less. You are probably wondering why I am expressing the filter loss in feet and not in psi for example. While it is possible and often done, it is simpler to use feet everywhere so that all the units are compatible. For those of you who want to know what the correspondence between feet and psi is, go to this link: https://www.pumpfundamentals.com/pump_glossary.htm#gl39
The fittings (i.e. elbows, tees, y's, etc.) friction loss in this case will be quite low and negligible, I don't expect we will have more than 2-3 elbows and this will offer very little resistance, less than 1 ft. The same applies to the valve that is located near the turbine; the resistance it offers when it is fully open is negligible.
The pipe friction loss HF can be determined in several ways. You can
use the web app that I have on my web site.
Calculations
In this section you can do your own calculations using a couple of equations and an applet on my web site. If you just need to get an idea of how much power you could generate with typical installation with 100, 500 or 1000 feet, see the charts that summarizes these calculations in Appendix A.
To calculate the pipe friction loss using the pipe friction loss applet, go to this link
https://www.pumpfundamentals.com/web-apps-1.htm.
You can put any pipe diameter size you wish for the calculation. Normally you want to use the inside diameter of the pipe as the pipe diameter. Depending on the construction and the pipe material, the inside diameter can be slightly smaller than the nominal size. So that a 3" pipe will vary between 2.9 to 3". I have used the nominal size as the inside diameter in all the calculations.
Let's start with a value of 200 gpm, 3" pipe diameter, 10 feet of head and a pipe length of 100 feet. We will assume that the piping will be made of steel, polyethylene or PVC or something equivalent. The type of material determines the roughness, the rougher the pipe the higher the friction. The materials mentioned all have a low roughness of approximately the same value, so leave the default values for roughness as in the applet.
Make sure you have 200 gpm in the flow rate text box and that all the other values. You will get a value for total friction loss HF of 9.9 ft.
Using 200 gpm we can calculate the velocity in the pipe based on the pipe diameter using equation (1)of 9.1 ft/s.
This is the velocity in the pipe, the velocity v2 is at the outlet of the nozzle which has a 1.5 in diameter outlet. Therefore we use equation (1) to calculate v2:
So now we put these values into equation (2)
We calculate v2 to be 2.3 ft/s and our assumption based on 200 gpm is 36.3 ft/s so that means that our assumption is wrong and we need to decrease the flow rate to get a better match.
The following table shows a series of calculations that converge on the correct value:
| q (USgpm) | HF from applet (ft) | Pipe velocity (ft/s) | v2 based on HF value (ft/s) | v2 based on equation 1 (ft/s) |
| 200 | 9.92 | 9.1 | 2.3 | 36.3 |
| 100 | 2.65 | 4.5 | 21.7 | 18.1 |
| 114 | 3.4 | 5.2 | 20.6 | 20.7 |
As you can see from the results in the above table the velocity in the pipe is quite low. This means that we may have a larger pipe than we need considering the available head. What would happen if we repeated this exercise with a smaller pipe size, say a 2" keeping the length the same at 100 feet. Also this time we will look at the amount of power provided by each of these scenarios. We will discuss later how power is calculated.
| q (USgpm) | H static head (ft) | HF from applet (ft) | Pipe dia. (in) | Pipe velocity (ft/s) | v2 based on HF value (ft/s) | v2 based on equation 1 (ft/s) | Power (watts) |
| 114 | 10 | 9.92 | 3 | 9.1 | 20.6 | 20.7 | 64 |
| 61 | 10 | 7.99 | 2 | 6.23 | 11.38 | 11.07 | 10 |
As you can see, we can save money on the pipe purchase due to the smaller diameter, but the power produced is also going down significantly. The 2" diameter pipe would not be a viable proposition.
The results of these calculations have been plotted and presented in three charts in Appendix A.
Power available
Now that we know the velocity and the flow rate at the end of the nozzle, we can
calculate the energy available, and therefore the power that is energy per unit time,
or Watts. There are two possible ways to calculate the power at the turbine wheel;
one is with the water jet velocity and the flow with equation (3); the other with
the head and the flow using equation (4). Both will give the same results. The head
h in equation (4) is the difference between the static head (z1 -
z2), and the friction loss, so that it is the net head at the water jet.
Rather than interrupt this article if you want to know where these equations come from see this pdf document![]() .
.
The power available is:
The Pelton turbine is designed to produce maximum power when the peripheral speed is 1/2 of the water jet speed. Therefore the power transmitted to the turbine wheel is 50% of the incoming water jet power. This is because the water jet is reversed by the wheel cup design 180 degrees back towards its source. The reversed water jet is not exactly in line so that the wheel itself has a real world efficiency of 90% or better. For a detail explanation of the power available at the turbine wheel see this link:
and also this link:
https://www.pumpfundamentals.com/micro-hydro_formulas.htm
and in our case
Our available power is 0.064 kilowatt or 64 watts.
The effect of static head
As you can see 10 feet of head does not provide a lot of energy. With more head, we can increase the flow rate through the pipe, and increase the velocity at the nozzle outlet, and thus provide more power. Of course the topography of the land must lend itself to this, the steeper the stream the better, so that you can get maximum elevation drop, for the shortest length of pipe.
The following table looks at these scenarios for different heads using a 4" pipe with static head varying between 25 and 150 feet and a pipe length of 500 feet with a nozzle diameter of 1.5":
| Static Head (ft) | Flow rate (USgpm) | Friction loss (ft) | Pipe velocity (ft/s) | Nozzle velocity (ft/s) | Water jet power (W) | Turbine wheel power (W) |
| 25 | 175 | 9 | 4.5 | 31.8 | 517 | 233 |
| 50 | 250 | 11.7 | 6.4 | 45.4 | 1509 | 679 |
| 75 | 306 | 26.1 | 7.8 | 55.5 | 2756 | 1245 |
| 100 | 355 | 34.7 | 9.1 | 64.4 | 4319 | 1944 |
| 150 | 437 | 51.8 | 11.1 | 79.4 | 8057 | 3626 |
KiloWatt-hours
It is interesting to know how much power you are producing and this is useful information to size the turbine, generator, and the electric cable. What is this power worth? The utility company charges vary but in my area they charge $0.07 per kW-h. In the scenario we studied you will be producing 64 watts on a constant basis. This means that every 24 hours, you are producing 64 X 24 = 1.54 kW-hours or in a 30 day month 46.1 kW-h. This would cost you $3.23 per month.
Table 5 gives a calculation for the power that your installation could produce at the generator shaft. It is based on the power of the water jet due to its mass flow rate, velocity and, the turbine wheel design, with its losses. This does not include the power loss at the generator or the normally negligible transmission loss through electrical cables (if sized correctly).
| Static Head (ft) | Flow rate (USgpm) | Friction loss (ft) | Pipe velocity (ft/s) | Nozzle velocity (ft/s) | Water jet power (W) | Turbine wheel power (W) | Power cost $ @ $0.07 per kW-h per month |
| 25 | 175 | 9 | 4.5 | 31.8 | 517 | 233 | $11.74 |
| 50 | 250 | 11.7 | 6.4 | 45.4 | 1509 | 679 | $34.21 |
| 75 | 306 | 26.1 | 7.8 | 55.5 | 2756 | 1245 | $62.74 |
| 100 | 355 | 34.7 | 9.1 | 64.4 | 4319 | 1944 | $97.96 |
| 150 | 437 | 51.8 | 11.1 | 79.4 | 8057 | 3626 | $182.74 |
Turbines are available with a number of nozzles varying from 1 to 4. The nozzle diameter determines the jet velocity. The main advantage of multiple nozzles is to reduce the velocity through each nozzle since there are many to share the total flow rate thereby diminishing wear due to high-velocity induced erosion. The power generated remains about the same.
Turbine speed
As explained earlier the Pelton turbine wheel is designed to run at half the water jet velocity, as this is where it will generate its maximum power. The turbine diameter must be matched to the jet velocity to achieve the proper rotational speed of the turbine wheel that turns the generator.
Based on the jet velocity the turbine rpm will be given by:
where d is the turbine diameter. In this case the turbine speed is:
Assuming the turbine diameter is 6 in, the turbine will turn at 1230 rpm with 100 feet of static head, 4" pipe and 355 gpm. This is a suitable speed for a permanent magnet generator. See this link https://www.pumpfundamentals.com/micro-hydro_formulas.htm to see how this equation was determined.
Turbine wheels come in different sizes and it is important to choose the right combination of diameter with the number of nozzles to obtain a suitable rpm for the generator to operate efficiently.
All these calculations have been pre-programmed in an Excel spreadsheet that you can
download at this address:
https://www.pumpfundamentals.com/micro-hydro_power.xls![]()
The equation used for calculating friction loss is the Swamee-Jain formula and you can find out about it at this web address: https://www.pumpfundamentals.com/help14.html.
All these calculations have been pre-programmed in an Excel spreadsheet that you can
download at this address:
micro-hydro_power.xls. ![]()
and in metric
and for those of you interested about how the applet solves for flow using the Newton-Raphson iteration
technique, see this document: Solving the gravity flow
equation for flow rate using The Newton-Raphson iteration technique
![]()
Turbine discharge
The water coming out of the turbine casing needs to be returned to the stream. It is in your interest to have a short distance, as this will reduce the pipe size required and minimize cost. This should be considered in you choice of location of the turbine. Again make sure that the pipe is layed out with a continuous slope towards the discharge and generously sized to avoid water build up in the turbine casing. You can use similar calculations to determine this pipe size, with the difference that there is no nozzle to consider.
Turgo wheel turbine
The Turgo wheel turbine is a variation on the Pelton turbine. The wheel looks like the Pelton wheel cut in half. Because the water jet interferes less with the wheel than the Pelton design it can handle more flow. They typically have 1 or 2 nozzles that are inclined at an angle with the plane (perpendicular to the shaft) of the wheel. Because the blade design is less complicated to manufacture it can be less expensive than the Pelton design. The application range is somewhere between 90 and 600 feet of head at the turbine.
Pipe pressure rating
This is a topic where there are some misconceptions. On many web sites the amount of power available is compared to the pressure at the bottom of the pipe due to the static head. This does not occur during the operation of a micro-hydro system because all the pressure energy due to height is converted to velocity (kinetic) energy, or friction loss. If you put a pressure gauge just ahead of the nozzle, you will read the pressure drop that occurs across the nozzle, since one end of the nozzle is at zero pressure. Depending on the design of this nozzle, the pressure drop can be negligible and there will be very little pressure at the bottom of the pipe, while the turbine is in operation.
However, if you close the turbine intake valve then the pipe will be under pressure due to the static head, and this produces the maximum pressure at the bottom. For 100 feet of head the pressure will be 100/2.31 = 43 psi. Therefore you should verify the pipe material maximum working pressure if the head of your system is above 100 feet. The pressure rating of the pipe should be at least the static head converted to pressure plus a reasonable safety factor.
Manufacturers of micro-hydro turbines
The Pelton turbine is one of the designs that is suitable for this type of application. The following images show the products offered by two manufacturers Harris and Hydro Power. Harris offers a range of turbine generators between 700 and 2500 watts.
Harris Hydroelectric is one manufacturer

Figure 7. Harris turbine.

Figure 8. Harris turbine view of the Pelton turbine wheel from below.
Figure 9. Hydro Power turbine view of the Pelton turbine wheel from below.

Figure 10. Hydro Power installation.

Figure 11. Turgo turbine.

Figure 12a. Turgo water jet nozzle position vs. wheel.

Figure 12b. Turgo water jet nozzle position vs. wheel.

Figure 13. Turgo wheel.
Appendix A
Analysis of the graphs of Power vs. Pipe diameter
The plots of power vs. pipe diameter are split into 4 graphs for systems that can be built with 100, 500, 1000 and 2000 feet of pipe. Single nozzles were used in the analysis and their diameter was optimized to give the maximum power for each static head and pipe size. The maximum nozzle diameter used was 1.5 inch.

Figure 14. Power vs, pipe diameter at 10-50 feet of head and 100 feet of pipe.

Figure 15. Power vs, pipe diameter at 25-150 feet of head and 500 feet of pipe.

Figure 16. Power vs, pipe diameter at 50-150 feet of head and 1000 feet of pipe.

Figure 17. Power vs, pipe diameter at 50-150 feet of head and 2000 feet of pipe.