Help for calculating pipe friction loss for any Newtonian fluid

Applets are programs based on the java language that are designed to run on your computer using the Java Run Time environment.

The following is an excerpt of the afore mentioned book. This java applet does friction head loss calculations for any Newtonian fluid for which the viscosity is known in the turbulent flow regime only which is most cases. The applet provides data on pipe roughness the source of which can be obtained in a pdf file at the bottom of this page.

PIPE FRICTION HEAD DIFFERENCE FOR NEWTONIAN FLUIDS

The Friction Head is the friction due to the movement of fluid in a piping system and is proportional to flow rate, pipe diameter and viscosity. Tables of values for Friction Head are available in references 1 & 8.

The Friction Head, as defined here, is made up of the friction loss due to the fluid movement and the friction loss due to the effect of pipe fittings (for example, 90° elbows, 45° bends, tees, etc.):

the subscript FP refers to pipe friction loss and the subscript FF to fittings friction loss.

NEWTONIAN FLUIDS

Newtonian fluids are a large class of fluids, whose essential property VISCOSITY, was first defined by Newton (see Appendix A for a list of Newtonian and non-Newtonian fluids). Viscosity is the relationship between the velocity of a given layer of fluid and the force required to maintain that velocity. Newton theorized that for most pure fluids, there is a direct relationship between force required to move a layer and its velocity. Therefore, to move a layer at twice the velocity, required twice the force. His hypothesis could not be tested at the time, but later the French researcher, Poiseuille, demonstrated its validity. This resulted in a very practical definition for viscosity.

The Darcy-Weisbach formula expresses the resistance to movement of any fluid in a pipe:

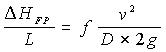
where f is a non dimensional friction factor. Often, the tables give values for friction loss in terms of ft of fluid per 100 ft of pipe. When the appropriate units are used (Imperial system), the Darcy-Weisbach equation becomes:

[3-16]

and in the metric system

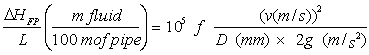[3-16a]

The friction factor is proportional to the Reynolds number which is defined as:

[3-17]

[3-17a]

The Reynolds number is proportional to the kinematic viscosity, the average velocity, and the pipe inside diameter. It is a non dimensional number. The kinematic viscosity is the ratio of the absolute viscosity to the fluid specific gravity SG.

Laminar flow - RE < 2000

Distinct flow regimes can be observed as the Reynolds number is varied. In the range of 0 to 2000, the flow is uniform and is said to be laminar. The term laminar refers to successive layers of fluid immediately adjacent to one another, or laminated. Looking at a longitudinal section of the pipe, the velocity of individual fluid particles is zero close to the wall and increases to a maximum value at the center of the pipe with every particle moving parallel to its neighbor. If we inject dye into the stream, we would notice that the dye particles maintain their cohesion for long distances from the injection point.

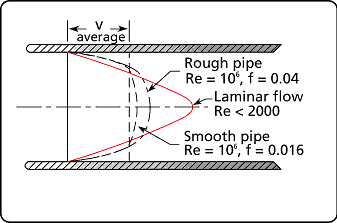
Figure 3-16 Laminar and turbulent flow velocity profiles.

The friction loss is generated within the fluid itself. Figure 3-16 shows that each layer (in this case each ring) of fluid is moving progressively faster as we get closer to the center. The difference in velocity between each fluid layer causes the friction loss.

The friction factor f is given by:

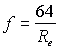[3-18]

For viscous fluids (i.e.: n > 50 SSU), the combination of velocity and viscosity usually produces a low Reynolds number and therefore laminar flow. Pumping viscous fluids at a faster rate may cause the fluid to become turbulent resulting in high friction losses. The tables for viscous fluid friction loss given in references 1 & 8 are based on the equation for laminar flow, equation [3-18]. This equation can be theoretically derived and is found in most fluid dynamic volumes (see reference 11). An interesting aspect of laminar flow is that pipe roughness is not a factor in determining friction loss.

Unstable flow - 2000 <RE <4000

The flow is pulsing and unstable and appears to possess characteristics of both laminar and turbulent flow.

Turbulent flow - RE > 4000

At Reynolds number larger than 4000, it is very difficult to predict the behavior of the fluid particles, as they are moving in many directions at once. If dye is injected into the stream, the dye particles are rapidly dispersed, demonstrating the complex nature of this type of flow. Reynolds, who originally did this experiment, used it to demonstrate the usefulness of a non-dimensional number (the Reynolds number) related to velocity and viscosity. Most industrial applications involve fluids in turbulent flow. The geometry of the wall (pipe roughness) becomes an important factor in predicting the friction loss.

Many empirical formulas for turbulent flow have been developed. Colebrook's equation is the one most widely accepted:

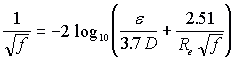[3-19]

where is the average height of protuberances (absolute roughness) of the pipe wall surface (for example, 0.00015 ft for smooth steel pipe). The term /D is called the pipe roughness parameter or the relative roughness. Since it is not possible to derive an explicit solution for f, L.F. Moody (see Figure 3-18) developed a graphical solution. The diagram shows the linear relationship of the friction factor (f) with the Reynolds number (Re) for the laminar flow regime. For Reynolds numbers in the medium range (4,000 to 1,000,000, turbulent flow), the friction factor is dependent on the Reynolds number and the pipe roughness parameter, which is known as the transition zone. For high Reynolds numbers (1,000,000 and higher, fully turbulent), the friction factor is independent of the Reynolds number and is proportional only to the pipe roughness parameter. This is the zone of complete turbulence.

Some typical values for the absolute roughness :

PIPE MATERIAL Absolute roughness
Steel or wrought iron	0.00015 ft
sphalt-dipped cast iron	0.0004 ft
Galvanized iron	0.0005 ft

Another equation developed by Swamee and Jain, gives an explicit result for f and agrees with the Colebrook equation within 1%, this is the equation used for this applet.

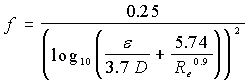[3-20]

The pressure head loss per 100 feet of pipe is obtained using equation [3-16]. You can get the total head loss by multiplying by the length of the pipe and dividing by 100. Then to convert to pressure loss, use equation [3-21].

[3-21]

A table of roughness values is available here.