August 2012
Pressure and its many facets
1.
The definition of pressure and how the weight of liquid causes pressure
2.
The difference between head and pressure
3.
Head, why is it used to describe pumps
4.
Liquids boiling at low temperature using low pressure
5.
Maximum vacuum level (what's the longest straw?)
6.
Low air pressure on Everest
7.
Cavitation in pumps and propellers
8.
Flotation (Archimedes principle)
9.
Air balloons, full of hot air and dirigibles
10.
The venturi
11.
Airplane wing (suspended with low pressure)
12.
Sail boat sail (sailing with low pressure)
13.
The barometer
14.
"Danger, danger Will Smith" the effects of low pressure in outer space
15.
Pressure variations within a piping system
16.
Air pressure in an aircraft
17.
Diving regulators
18.
Caisson workers or compressed air workers
19.
Pressure testing
Pressure is everywhere. This is a few of the areas where it acts and affects our lives from meteorology to the vacuum of outer space. In the Victorian era they said that "Nature abhors a vacuum" implying that a natural vacuum could not exist. Well, it's easy as pie to create a vacuum just use a straw to imbibe your favorite drink.
1. The definition of pressure and how the weight of liquid causes pressure
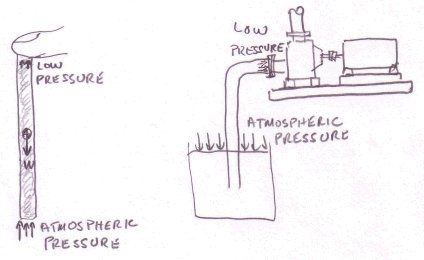
Pressure is the state of a liquid or gas under compression, typically the pressure within the container is higher than the outside environment but occasionally it can be less. We will be concentrating on liquids; the difference between liquids and gases is that liquids are incompressible, under pressure their volume does not change contrary to gases where the volume changes considerably. Also liquids are much denser than gases so that the amount of vertical height of liquid above a given point is important as the weight of liquid on its own will create pressure at that point; this is not the case with gases. If you move an object up or down within a liquid column the pressure it is exposed to will vary, there will be less pressure near the surface because the weight of liquid above the object is less and more when the object is lower.
One way to think of pressure is to visualize tiny force vectors acting on an object suspended within the liquid. Where the liquid is in contact with a surface the force vectors are perpendicular to the surface, this is because liquids have no capacity to maintain shear forces on a surface.
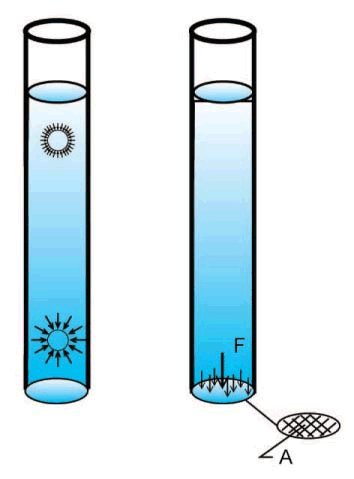 Figure 1
Figure 1
By definition pressure is a force divided by area: p = F/A. Not all forces are point forces, so this is a way to understand the effect of distributed forces on objects such as: the effect of air pressure on stretching a balloon, the effect of the weight of a house on a foundation and the pressure generated under the foundation, or the effect of a force on a cylinder to create pressure in a combustion chamber of a car engine.
Imagine that the object is a flat disk on the bottom of the tank, very flat and the same diameter as the tank bottom.
What is the pressure on the disk? The force F will be the weight of the liquid on the bottom of the tank and that area
A the area of the bottom of the tank. The force F is equal to the density times the volume or F = dens. x V (density is weight per
unit volume) or if I replace the term "dens." by the Greek letter rho (ρ) then F = ρ x V. The density of water at
standard conditions is 62.34 lbf/ft3 or 1000 kg/m3. Therefore the pressure at the bottom is ρ = F/A = ρ x V/A, and
since V = h x A then V/A = h, therefore p = ρ x h, a very nice simple formula that gives pressure related to depth and
the density of the liquid. The pressure varies for a given position depending on the density of the liquid. The pressure also
varies for a given liquid depending on the vertical position.
A common representation of this formula with appropriate units in the Imperial system is:
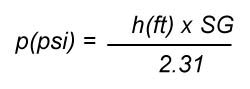
SG is the specific gravity of the liquid which is the ratio of the density of the liquid to the density of water. For water, SG has a value of 1. This is easier to remember than 62.34 lbf/ft
3.
Let's try an example, what is the pressure at the bottom of a pool 10 feet deep.
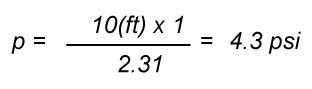
2. The difference between head and pressure
Pressure can be measured by pressure gauges. They are often located on pump discharges. Why? Because the pressure level will determine (along with other factors) the flow rate of the liquid through the system.
Head is a term used in pumping systems and is a convenient way to describe the work that a pump can do via the pressure that it develops. The capacity of a pump is typically given in terms of head and flow. For a centrifugal pump head varies with flow, when the flow is zero the head is at maximum and when the flow is maximum the head is at a minimum. For example, if a pump has a maximum head of 50 feet (15.2 meters) then it can get a liquid to a height of 50 feet with respect to the surface of the water in the suction tank. There may be no flow coming out of the pipe but the liquid will get to 50 feet. To produce flow, the head will have to be less than 50 feet, and this means that the discharge point will have to be lower than 50 feet (see Fig. 2).
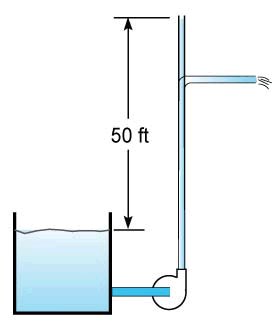 Figure 2
Figure 2
A centrifugal pump is a device that creates pressure. It does this by moving water (using the impeller) in a circular channel
(the pump casing) at high speed; the centrifugal force created by the circular motion is converted to pressure. The result is
that the pressure at the outlet of the pump is higher than at its inlet.
(see this simulation of how a pump impeller acts on fluid particles and produces
pressure:
https://www.pumpfundamentals.com/pump_glossary.htm#gl11_1)
The pump manufacturers do not know what type of water source the pump will be connected to; it may be that the pump is connected to a high tank providing lots of pressure to the pump inlet, this is a system with a high suction static head. The reverse can also be the case and this is a system with a low suction static head. (see Fig. 3)
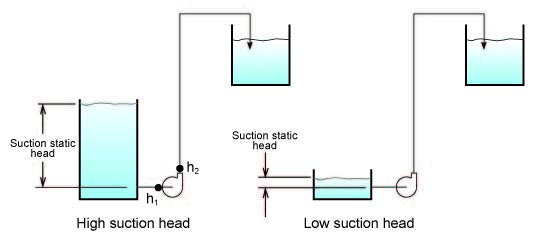
Figure 3
To account for this, the head value manufacturers provide is always a difference of head between the outlet and inlet of the pump
(known as total head (TH = H
2 - H
1 see Fig. 3). In this way they are independent of what is connected to
the inlet and outlet and provide only information pertinent to the pump. This allows the user to determine what head will be
available at the pump outlet since it is known how much head there is at the inlet of the pump. Therefore the head at the outlet
of the pump is
(H
2 = TH + H
1).
Why does the user need to know the head at the outlet of the pump? Because it will determine the flow rate of the liquid through the system. This flow rate will depend on the height to be reached (static head) and the velocity within the pipe as well as the diameter of the pipe (friction head). The sum of static head and friction head on the discharge side of the pump must be equal to the head at the outlet of the pump. If they are not equal then you have to either change the pump, or change some characteristic of the system, flow rate or pipe diameter, or static head, or a combination of these.
Sometimes it useful to know how much pressure difference corresponds to the total head of the pump. It is a simple formula that can be hard to remember especially in North America where the units are often in metric or Imperial.
The relationship between head and pressure in the Imperial system is:
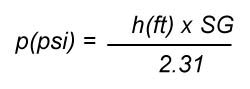
where SG is the specific gravity of the liquid (for water SG = 1). The unit of pressure is psi or pounds per square inch and the unit of head is in feet in the Imperial system. Specific gravity does not have a unit because it is the ratio of the density of the liquid to the density of water at standard conditions. The metric version of the head vs pressure formula is:
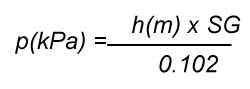
The unit of pressure is kPa or kiloPascal and the unit of head is in meters in the metric system. These are the two most commonly used units for pressure and head in the Imperial and metric system of units.
There are other uses for converting head to pressure for example, the difference in pressure across a control valve, occasionally this is given as a difference in head and other times as a difference in pressure.
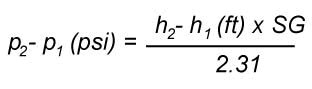
Sometimes the head will correspond to a quantity measurable with a tape measure such as the static head of a pump system which is the difference between the elevation of the outlet of the system versus the elevation of the suction tank fluid surface (see Fig. 4).
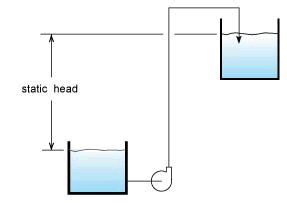
Figure 4
3. Head, why is it used to describe pumps
Head is another way to describe the amount of energy in a system. For example in Figure 4 we see a system with a high static head. There is allot of energy stored by having water located in a high place, imagine if the tank drain were to be opened all this energy would be released, if you put a turbine at the bottom end of a drain pipe you could extract allot of energy out of the flow of liquid.
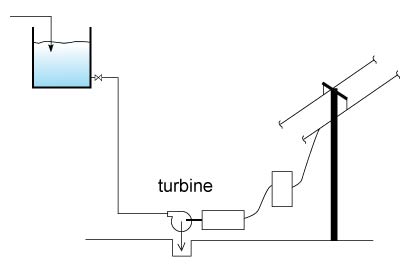
The static head informs us on the amount of energy stored in a high place or the amount of work required getting that liquid to a higher level. This energy storage method is used for load balancing in power stations to utilize off-peak hour energy and be more cost effective, see this article in Wikipedia:
https://en.wikipedia.org/wiki/Pumped-storage_hydroelectricity .
From this point on work and energy are terms that are used interchangeably. They have the same units, historically work has been used to express the amount of energy that a person or device must produce to accomplish a task. Energy has often been used to express the amount of energy available such as water stored at a height, the energy in a flowing river, wind energy, etc.

How does this relate to our everyday experience? If someone lifts a weight off the ground to a position 6 feet up we do not say that he has expended an amount of energy proportional to 6 feet.
We say that he has lifted a weight 6 feet vertically upwards. To be more precise we will specify the weight, say 100 pounds (lbs.) and we could then say that the amount of work done is 100 x 6 = 600 ft-lb, the ft-lb is a unit of work. Another unit of work is the calorie and 1 calorie is equal to 3095 ft-lb, so that 0.2 calories have been spent to raise the weight. So we see that the amount of work or energy spent by a person to accomplish a certain task tells us allot about the size and the ability to do work.
Let's go back to the term head and take it apart. The unit of head is feet or meters in the metric system, how does this relate to work? The head unit of feet can be derived by combining two other units: work and weight. Head can be expressed as thwe ratio of work over weight:
head (ft) = work (ft-lb)/weight (lb), the weight unit cancels and we are left with head in feet.
Head is a convenient way to say work per unit weight or how much work is required per unit of weight of the object being displaced. This unit of work per unit weight is called specific energy.
So now we have a convenient way to describe how much work is required per unit weight of liquid to do a certain task such as lifting liquid up to a height. So that 50 feet of head really means that it takes 50 ft-lb of work per lb of liquid to raise this liquid to a height of 50 feet as in Figure 2. The next thing to determine is how fast can we do this job?
How does this apply to moving liquids? We never say that we have moved so many pounds of liquid up a certain height. Why? Because it is not the weight of liquid displaced that interests us but the volume displaced. If I want to fill up a pool I don't say I need to transfer 930 tons of water, I will say I need 4,000 cubic feet of water to fill this pool (1 cubic feet = 7.48 gallons) or 29,000 gallons. And since I am not willing to wait 5 days to do this job I may want to be able to transfer the water in a period of 8 hours so that the rate of transfer is 29,000 gals. over 8 hours or 29,000/8 = 3700 gals/h (gph) or a more typical unit is gals/minute (gpm) which then becomes 3700 / 60 = 62 gpm. So for me a reasonable transfer rate is 62 gpm and I need to find a device or source that can give me that rate.
Now we have two characteristics head and flow that describe the action of a pump (head in feet or the amount of work per weight of liquid displaced) and flow ( the volumetric flow rate in gpm or how fast can we do the transfer). And this is exactly how pump manufacturers describe the ability of pumps to do a certain job.
Typically they will supply a pump performance curve which is a graph of head vs. flow for a certain size pump (i.e. impeller diameter and rotation speed).
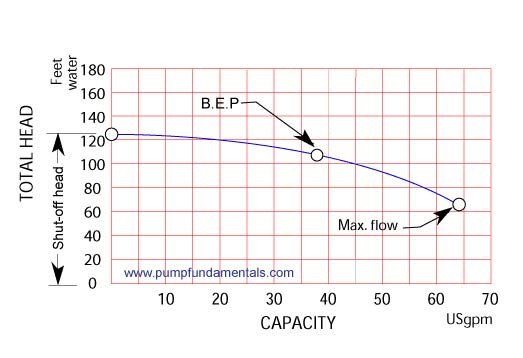
Normally we want to operate the pump somewhere in the middle of its curve close to the B.E.P. or best operating point. This is a point where the pump operates at its maximum efficiency. We see that as we reduce the flow, possibly by closing a valve on the pump outlet the operating point moves to the left on the curve until it reaches zero flow if the valve is closed completely. This point is known as the shut-off head of the pump, at this point we will have the maximum head the pump can deliver at zero flow similar to the situation we described in Figure 2 where we attain zero flow by lifting the discharge pipe end until the flow stops. We can operate the pump at the end of its curve; this will provide the maximum flow at the minimum head assuming that we can run liquid through the system at this maximum flow and minimum head.
The pump should be selected in such a way that it operates near its BEP head and this head corresponds to the static head plus friction head losses in the system at a given flow rate.
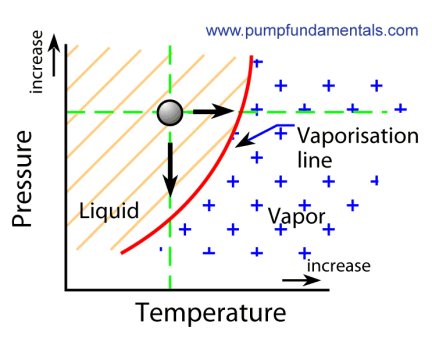
4. Liquids boiling at low temperature using low pressure
There are two ways to boil a liquid, one is to raise the temperature until boiling occurs, in the case of water under
normal atmospheric pressure boiling will occur at 212 deg. F or 100 deg. C. You do this every day when you boil water
on a stove. The other way is to lower the pressure while keeping the temperature constant. The water must be in a
sealed container and the pressure lowered by means of a vacuum pump or other means. For water at room temperature
boiling will occur at 1 or 2 psia. It is quite amazing to see water boiling at low temperature, it goes against
all our experience, see this video on youTube:
https://www.youtube.com/watch?v=EN2_IibETns 
Vapor pressure is the physical property that tells us at what pressure a liquid will boil for a given temperature. This will vary depending on the liquid, very volatile liquids such as acetone will have a very high vapor pressure (evaporates easily) for a given temperature and others such as mineral oils will have a low vapor pressure (evaporates with difficulty).
5. Maximum vacuum level (what's the longest straw?)
Vacuum is a lack of pressure as compared to atmospheric pressure. Sometimes vacuum is expressed in pressure units and other times in head units.
What is the head that corresponds to atmospheric pressure? Atmospheric pressure is 14.7 psia at sea level, the "a" stands for absolute. Normally "psia" is not used because we have the normal atmospheric pressure all around us and we only need to know how much greater than atmospheric the pressure is. This unit is known as the "psig", no doubt for psi gauge therefore 0 psig = 14.7 psia.
What is the equivalent of 14.7 psia in head? Assuming we are using water, if I put the value of 14.7 in the pressure to head formula with SG =1, p = h/2,31 or h = p x 2.31, I get 14.7 x 2.31 / 1 = 34 feet. What is a physical representation of this?
If you have a tube 34 feet long full of water and you close one end and raise this end vertically until the whole tube is suspended off the ground. Then right under the capped end of the tube the pressure will be 0 psia and the liquid will be suspended within the tube. This is because the atmosphere exerts pressure on the open end of the tube and is capable of supporting 34 feet when its value is 14.7 psia. This is the same effect shown in barometer except the a barometer uses mercury which is 14 times as dense as water so that the height of the column can be much shorter (see the section on the barometer).
Some pressure gauges have a dual scale, one to measure pressure above atmosphere and the other to measure pressure lower than atmosphere (vacuum). These are sometimes located on pump suction lines and can be useful when on occasion the level in a suction tank is low resulting in vacuum at the pump suction.
6. Low air pressure on Everest
Why do climber's need supplemental oxygen when climbing high mountain peaks such as Everest. The pressure decreases with altitude, at 29,000 feet which is the height of the summit of Everest the atmospheric pressure is only 5 psia. This means that the amount of air molecules contained in a given volume of air is much less than it is at sea level and we need oxygen to live. Therefore supplemental oxygen is required for most people unless you are extremely fit and well acclimatized.
7. Cavitation in pumps and propellers
If you have ever a heard a pump that sounds like it is pumping rocks this is due to cavitation. When the pressure is low at the inlet of a pump this is when cavitation can occur. The pressure can be low for any number of reasons: an obstruction in the pump suction line, low water level in the suction tank, and anything else that can cause low pressure at the pump suction. Low pressure causes the liquid to vaporize forming bubbles on the underside of the impeller near the suction eye; as pressure builds up due to the action of the rotating impeller, the bubbles collapse causing this characteristic gravelly noise.
 Want to hear the sound of cavitation.....!
Want to hear the sound of cavitation.....!
In the case of the propeller, none of the causes for low pressure mentioned above apply, however if the impeller is improperly shaped or rotating to fast, low pressure can also be created resulting in cavitation.
8. Flotation (Archimedes principle)
Archimedes was the first to state the principle of flotation. I am paraphrasing but it goes something like this: "A body floating on a water surface will displace an amount of water corresponding to it's weight." If you put an object in water that floats, meaning that its overall density must be less or at least equal to that of water then it will displace an amount of water equal to its weight.

How could Archimedes have figured that out? Well I am speculating but possibly by observation, then by experimenting and then generalizing (the old scientific method, it was really old then). The observation is that all floating objects displace a certain amount of water. Is the shape of the object critical to floatation? Not really, even a crude rough block of wood will float. More water is displaced depending on the weight of the object, in other words a heavier ship sinks lower into the water. Archimedes had the insight that perhaps the weight of water displaced exactly balanced the weight of the object. How could he verify this? One way is to do an experiment with models and using a tub of water that is exactly full in such a way that any object placed on the surface will make it overflow. If you lay some object on the surface, perhaps a model of a ship and you collect the water that has overflowed from the tub, you can put the water on one side of a balance and the object on the other and see if the weights are equal or not. Of course you have to take into account the weight of the container of water. I can imagine that Archimedes did this experiment with many different models of different shapes and weights and always got the same result. He therefore generalized to all classes of floating objects.
Today, we can figure all this out by using some basic physics. Let's take a simple object like a square block of wood and imagine that it is floating on water. Can we figure out how far down in the water the object will be and does the amount of water displaced equal its weight?
We know that pressure increases as the depth increases. The pressure p is the ratio of a force F divided by an area A. We call the water density ρ
W so that
p = F/A ; F = ρ
W x V; therefore p = ρ
W x V / A; V/A = h
Therefore p = ρ
W x h where ρ
W equals 62.34 lbf/cu.ft. and h is the depth.
The weight of the object W will be balanced by the force created by a pressure at a certain depth, h for example. The force F that's holding the object up will be equal to the pressure below the object times the surface area (b wide x C long), or F = p x A = dens. water x h x (b x c) and F is equal to the weight of the object W, F = W since the object is not moving in the vertical direction. Therefore W = dens. water x h x (b x c); of course h x (b x c) is exactly the volume of water displaced therefore we have proved that the object's weight is balanced by the weight of water displaced (see Fig. 5).
How far down will the object go down into the water? This will depend on the density of the water and the weight of the object. We can use the same equation to calculate the depth h, h = W / ρ
W / (b x c) where b is the width and c is the height.
We stated that another requirement for the object to float is that its density be less or at least equal to that of the surrounding medium, in this case water. The weight of the object W will be equal to
W = ρ
o x d x (b x c) where d is the length of the object. For W to be equal to F;
W = F
or
ρ
o x d x (b x c) = ρ
W x d x (b x h),
we see that if c is greater that h, that is the object is partly above water then the density of the object must be less than that of water to make the equation balance. And if h equals c and the top of the object is exactly even with the surface then the density of the object must be the same as that of water.
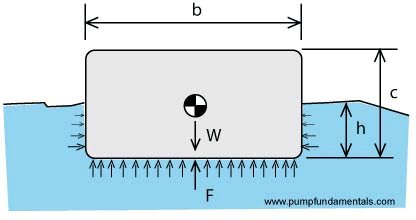 Figure 5
Figure 5
9. Air balloons, full of hot air and dirigibles
Air balloons are filled with hot air and the air is kept hot by using a gas burner located at the bottom of the balloon. This large mass of air is at a lower density than the surrounding air. As we know from the section on "Archimedes principle", objects that have a lower density than the surrounding medium in this case air, will float or in this case rise. When the air is at the proper temperature the overall weight of the balloon, basket, people and burner will just balance the overall external air pressure and the balloon will be in equilibrium or level flight.
 Permission for the use of this figure has been requested
Permission for the use of this figure has been requested
Dirigibles are usually filled with helium and the bags containing the helium are hermetic. Helium is a gas that is lighter than air at room temperature. There has to be enough helium at the start to balance the fully loaded dirigible plus the ballast. The ballast is often water and is dropped from the dirigible when it becomes absolutely necessary to gain more lift. Otherwise the dirigible is always at equilibrium with the surrounding air.
10. The venturi
A venturi is a pipe that has a gradual restriction
that opens up into a gradual enlargement. The area of the restriction will have a lower pressure than the
enlarged area ahead of it. If the difference in diameters is large you can even
produce a very high vacuum (-28 feet of water). I use a cheap plastic venturi made by Fisher or Cole Palmer
for an experiment that I do to demonstrate vapor pressure during my training seminars and it is very
easy to create very high absolute vacuum.
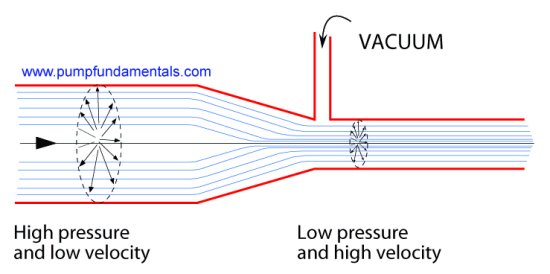
It is not easy to understand why low pressure occurs in the small diameter area of the venturi. I have come up with this explanation that seems to help.
It is clear that all the flow must pass from the larger section to the smaller section. Or in other
words, the flow rate will remain the same in the large and small portions of the tube. The flow rate
is the same, but the velocity changes. The velocity is greater in the small portion of the tube. There
is a relationship between the pressure energy and the velocity energy, if velocity increases the pressure
energy must decrease. This is the principle of conservation of energy at work which is also Bernoulli's law.
This is similar to a bicycle rider at the top of a hill. At the top or point 1 (see Figure 6 below), the
elevation of the cyclist is high and the velocity low. At the bottom (point 2) the elevation is low and the
velocity is high, elevation (potential) energy has been converted to velocity (kinetic) energy.
Pressure
and velocity energies behave in the same way. In the large part of the pipe the pressure is high and velocity is low, in the
small part, pressure is low and velocity high.
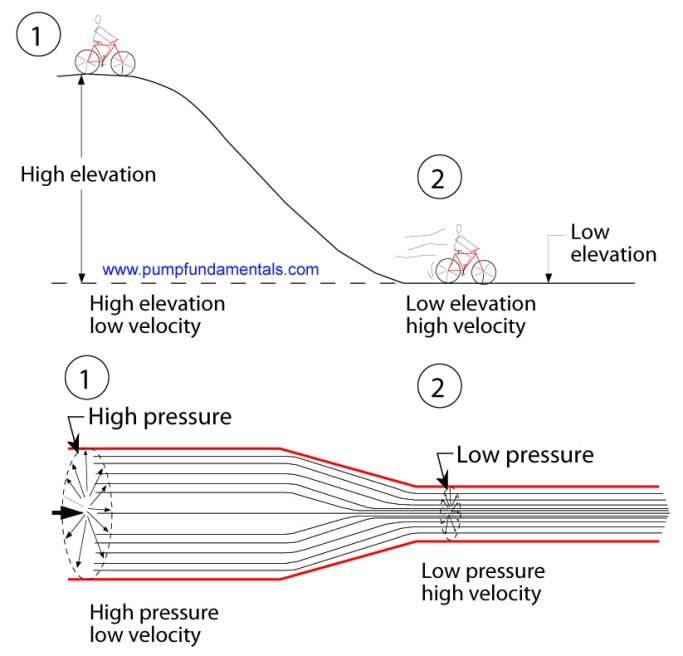
Figure 6 The venturi effect.
Bernoulli's law is a relationship between two points within a system that states that the sum of the
energies that correspond to pressure, velocity and elevation must be conserved.
The general form of the law (neglecting friction) is:
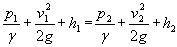
where p
1 is the pressure, v
1 the velocity and h
1 the elevation
at point 1 and the same parameters are used at point 2. Gamma
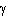
is the fluid density and g
the acceleration due to gravity.
In the case of the cyclist there is no pressure and only the velocity and elevation can vary, so that
Bernoulli's law becomes:
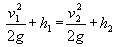
as the cyclist goes down the hill h
2 becomes smaller than h
1 and to
balance the equation then v
2 must be larger than v
1.
In the case of the venturi tube there is no elevation change and only the velocity and pressure can vary,
so that Bernoulli's law becomes:

We can clearly see that if v2 is greater than v1 then p2 must be smaller than v1 to balance the equation.
see this video on youTube:
https://www.youtube.com/watch?v=DaXtJ67x1To 
11. Airplane wing (suspended with low pressure)
An airplane is not so much pushed up by the air it travels through as suspended. The movement of the air around the aircraft wing causes low pressure to be generated on the top of the wing with respect to the bottom of the wing. This difference in pressure generates a net upward force that keeps the plane in the air. The engine can then move the plane forward by rotating a propeller.

and what say the bird wing...
 Permission for the use of this figure has been requested
Permission for the use of this figure has been requested
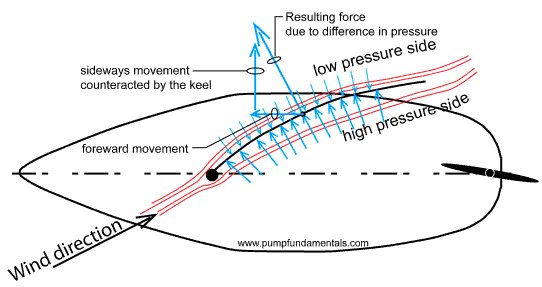
12. Sail boat sail (sailing with low pressure)
A sail has similar cross-sectional shape than an airplane wing, it's like a wing turned vertical. The difference in pressure from one side to the other of the sail pushes or you might say pulls the boat forward or sideways depending on the angle of the sail with the boat.
13. The barometer
The barometer is an instrument that measures air pressure. The fall and rise of air pressure correlates with the weather as low pressure is likely to bring high winds and rain so that it becomes an important tool in meteorology.
Traditionally barometric pressure has been given in inches of mercury in the Imperial system. If we put a column of mercury in a sealed glass tube (see Fig. 7), we can calculate the height needed to balance the atmospheric pressure using the formula above. For this we need to know the specific gravity SG of mercury which is 14 meaning that mercury is 14 times as dense as water. When the pressure is 14.7 psia we get a value of 14.7 x 2.31 / 14 = 2.42 feet of mercury or 29.3 inches which is the way barometric pressure is given in the Imperial system. In the metric system, the kilopascal pressure unit has been constructed such that 100 kPa represents approximately 14.7 psia.
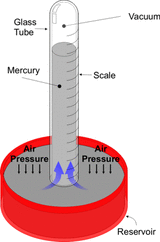 Figure 7
Permission for the use of this figure has been requested
Figure 7
Permission for the use of this figure has been requested
14. "Danger, danger Will Smith" the effects of low pressure in outer space
Much has been written about this or played out in science-fiction movies. Bur really what is likely to happen if you are in outer space, space walking outside your capsule for example, and your space suit springs a leak? All your water based fluids will vaporize or form bubbles in a similar fashion to that seen in the section on "Boiling water at low pressure". For example blood is 55% plasma and plasma is the yellowish fluid that carries red and white blood cells. Plasma is 80% water. Therefore you will get large vapor bubbles in your veins and arteries and your blood will cease to flow very rapidly giving you only minutes to live. And of course there will be many other effects that will be very annoying.
15. Pressure variations within a piping system
Many people make the mistake of thinking that because a liquid is pumped there is positive pressure everywhere within the system. The pump is merely the engine that creates pressure allowing liquid to flow to areas that it would not flow to by itself (gravity assisted for example) otherwise. Pressure will vary throughout the system depending on the height and pressure loss due to friction from a high level at the pump outlet to atmospheric level or zero at the system outlet, assuming the system has an open outlet pipe. As you go up pressure drops because there is less weight of liquid at a higher elevation, therefore expect to have low pressure, lower than the pressure at the outlet which is typically zero. If you make the mistake of trying to put a connection at this location so that you can divert some flow to another area, not only will you not get flow but air will be sucked in disrupting your system.
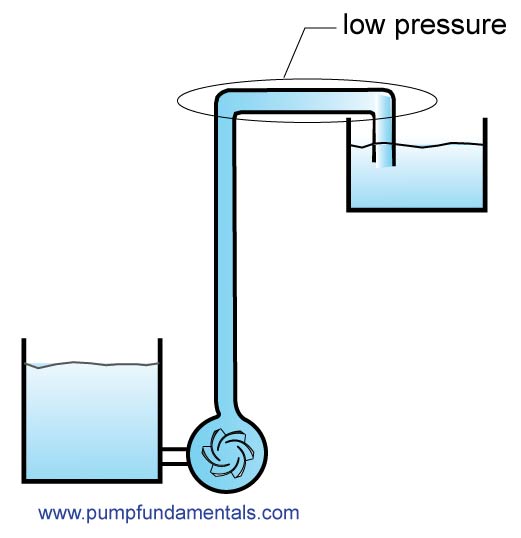
16. Air pressure in an aircraft
Modern aircraft fly at an altitude of 35,000 feet, the air pressure outside the aircraft at this altitude is very low, approximately 3.5 psia, therefore the plane must be pressurized for the comfort of the passengers otherwise you would have to strap on a scuba diver's tank. However, it is not fully pressurized to the level we are accustomed to on the ground; it is pressurized to about 11 psia which is 5 psi less the pressure at sea level. This corresponds to an elevation of 8,000 feet and if you were a climber you would probably be comfortable at that elevation without supplemental oxygen. After all Mexico City is at 8000 feet elevation. Aircraft manufacturers do this to reduce the amount of material required to keep the integrity of the hull, if they fully pressurized the plane the hull would have to be much thicker to balance the lack of pressure on the other side of the aircraft and therefore the plane would be heavier. It seems that they have established that most people are comfortable at this pressure level and that's why you feel your ears popping when you go up and down in altitude because the air pressure within the aircraft is changing. However the Boeing Dreamliner is pressurized to the equivalent of 6000 feet (11.8 psia) the strength of the hull is increased using carbon fiber and related technologies. Boeing says that passengers have fewer headaches and feel better.
17. Diving regulators
A diving regulator provides air to the diver as he descends below the water surface. As we know pressure increases as we descend. Using the formula above we see that the pressure increases by 4 psi for every drop of 10 feet. This is why your ears hurt when you dive to the bottom of a swimming pool, the air inside your throat is at lower pressure that on the outside of your ear drum caving it in and causing pain.
The solid parts of our bodies are made of 60% water and water is incompressible, therefore an increase in pressure is not physically affecting or compressing those parts, the other hard parts such as bone are also very hard and incompressible. However there are areas in our bodies that contain gas such as our lungs, our stomach and intestine and our inner ear. There is not much that can be done about the ears because these are uncovered and not connected to the regulator other than from the inside of our throat. We use air pressure from inside our throat to balance the pressure from the outside to keep our ear drums from collapsing and reduce the pain. If you have ever done any scuba diving you know how critical this is.
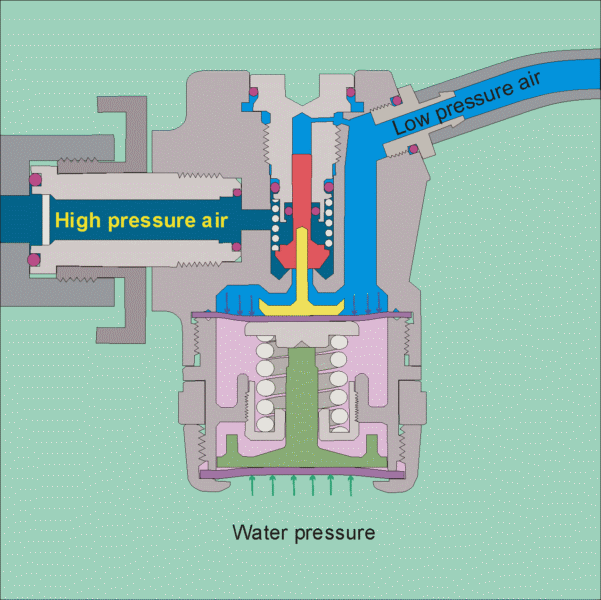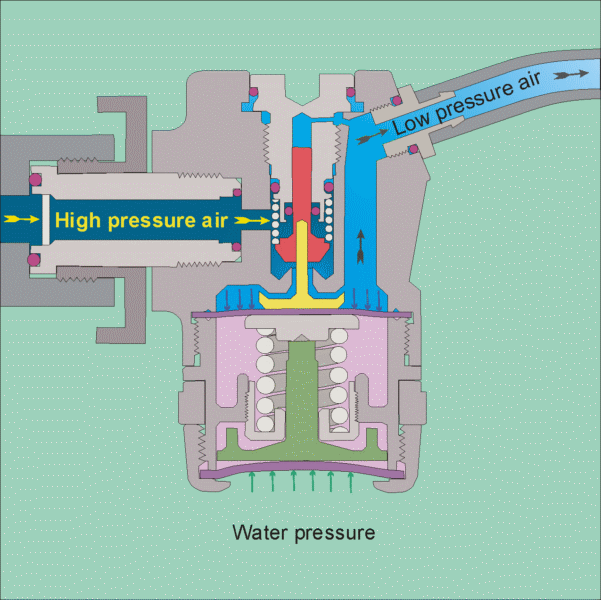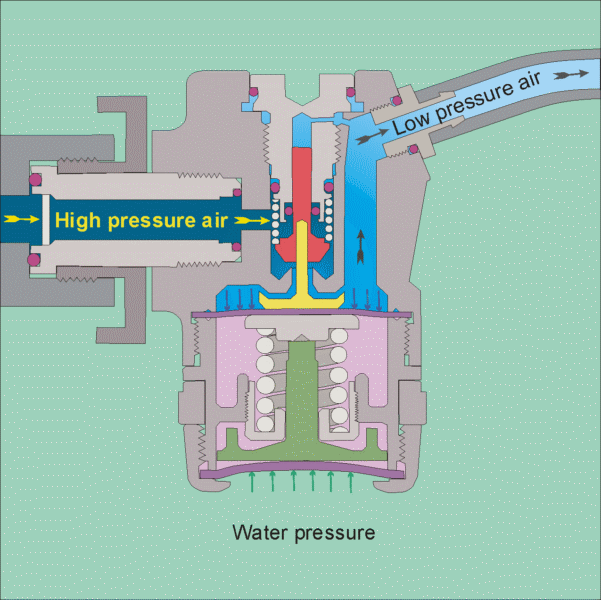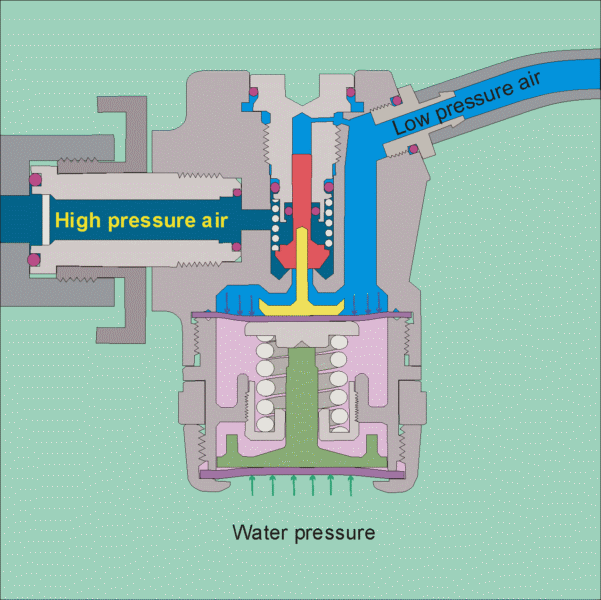
The air tank pressure is around 125 psi, so that there is plenty of pressure for diving to the depths that most recreational divers go to (100 feet being a typical limit). The regulator has 2 stages, the 1st stage reduces the pressure to the ambient level, so that if you are at 10 feet the pressure will be 4 psig and if you are at a 100 feet it will be 40 psig. It does this by using cleverly designed diaphragms in conjunction with springs to balance the air pressure with the water pressure (see this site for images of the operation of a regulator
https://www.diveboard.com/community/technics/2011/02/know-your-gear-the-regulator/). The 2nd stage is in the mouth piece and its function is to allow air into the mouth and lungs on demand and also allow exhalation on demand. Since the pressure within the lungs is the same as the surrounding environment this can be done.
 Permission for the use of this figure has been requested
Permission for the use of this figure has been requested
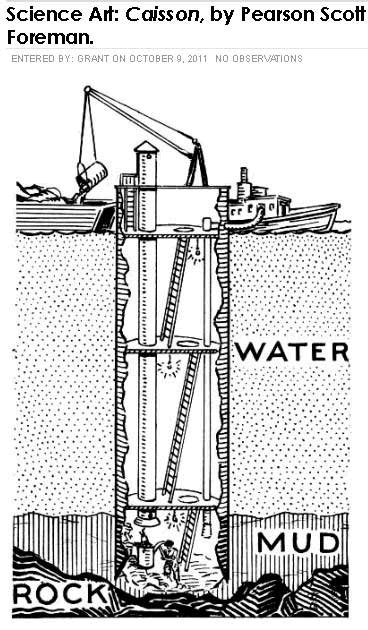
18. Caisson workers or compressed air workers
Caissons are containers that are lowered into the water to allow workers to work on a river bed when building foundations for a bridge for example. The caisson is air tight and sealed at the top, it is lowered onto the river bed and then pressurized air is piped into it to remove the water and keep the caisson dry. Workers come in and out of the caisson via an airlock. The pressure in the caisson must be high enough to overcome the pressure at the bottom of the river. As we know from our formula that if the river bottom is 50 feet below the surface that the pressure must be at least 50 x 2.31 / 1 = 22 psig. Therefore workers must work in an environment where the pressure is higher than where they normally live, it's the same high pressure environment of scuba divers. In the early days of this type of work such as when they built the foundations for the Brooklyn bridge workers would get the bends which is the same condition that divers get if they go to depth and come back up too fast. The problem is that when you stay at depth for a significant period of time the nitrogen in your lungs enters into solution within your blood and when you come up too fast large nitrogen bubbles come out of solution causing embolism and serious pains in the joints and other adverse effects. The same techniques such as breathing a mixture of helium and air that keep deep sea divers safe today are now also used to protect caisson workers.
19. Pressure testing
Pressure testing is required for pipes, tanks or other devices that convey gas or liquids under pressure.
The code that regulates this is the ASME Boiler and Pressure Vessel code for North America. This code
came about as the result of many boiler failures and the resultant deaths and injuries that occurred
in the mid-1800's when strict guidelines were not available. The code specifies the types of materials
that can be used and the pressure rating that can be achieved for various thicknesses depending on
the application. Vessels are fabricated in accordance with the code. It also specifies what is
considered a pressure vessel; a vessel that is subjected to 15 psig or more internal or external pressure.
A pressure test is required to ensure the safety of an installation. This test is normally
done with water or air at a pressure of 1.3 to 1.1 times the operating pressure and is called
a hydrostatic test. The length of pipe or vessel being tested is isolated as appropriate to
the situation (i.e. blinded valves, blinds on flanges or other). The test is successful
when the pressure can be maintained for the duration of the inspection after the source
is removed. Water is normally used; air or nitrogen can be used but is discouraged. Why?
You can store up 200 times more energy for the same pressure and volume using air than
water because air is compressible. If there is a catastrophic leak the release of energy
from the equipment under air (pneumatic) test will be much more dangerous that if
water were used, seems counter intuitive.
 Permission for the use of this figure has been requested
Permission for the use of this figure has been requested
 Permission for the use of this figure has been requested
Copyright 2019, PumpFundamentals.com
Permission for the use of this figure has been requested
Copyright 2019, PumpFundamentals.com



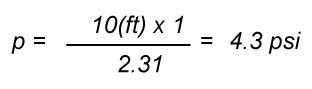


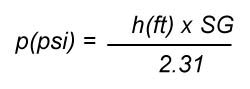
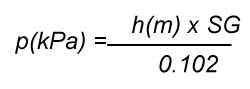
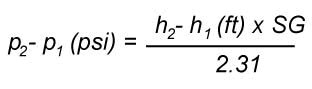











 Figure 6 The venturi effect.
Figure 6 The venturi effect.









