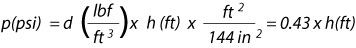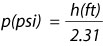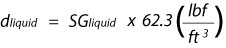Pressure or head

Download this article in pdf format pressure and static head

What is the relationship between head and pressure? Let's take the static case, no moving liquid.

What is the relationship between the pressure level at the bottom of a tank and the height of liquid above it? The weight of the liquid W distributed over a surface A will provide the pressure. Pressure is a very useful concept in liquids because there is no solidity to liquids, you can't push on them, fluid particles just slip by one another. But they will have an effect on their boundaries which can be expressed as pressure.

By definition

p = W/ A

The weight of the liquid will be defined by its density in lbf / ft³ for example times the volume V.

Density in this case is a constant and for water it is equal to 62.3 lbf/ft³ at a reference temperature.

W = dens. x V

The volume V depends on the height and the surface area of the volume that contains it:

V = A x h

Therefore

p = W / A = dens. x A x h / A = dens. x h

Now let's put consistent units on these quantities, p in psi, h in ft and density in lbf/ft³ and let's just call density d.

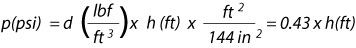
Let's take the reciprocal of 0.43 and we will get the familiar constant 2.31:

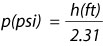
This applies for water but many liquids have different densities, they can either be heavier or lighter for the same volume. To express this we use the term specific gravity or SG. The value for SG expresses how many times the liquid is heavier than water per unit volume. SG for water is 1.0, fuel oil has a specific gravity of 0.893 so it is lighter than water and will float on top; sulphuric acid at 100% concentration has an SG of 1.84. When you want to find the density of a liquid and you know its SG:

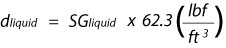
Putting this definition for SG in the formula above we get:

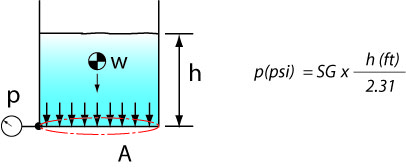
Containers or tanks come in different shapes. How will the shape affect the pressure at the bottom? Let's look at all these different shapes and see how the pressure at the bottom varies with the liquid level height.

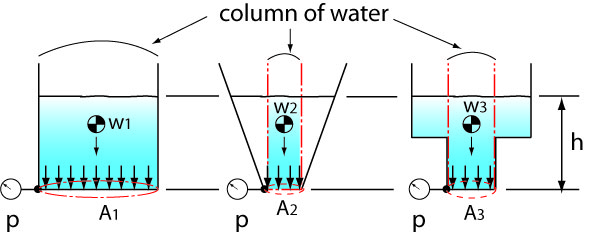
The force vectors that are the source of pressure are always perpendicular to the surface, that's because the liquid is not capable of maintaining tangential forces in a static condition. Therefore the weight that presses down on the surface is coming directly from above and is called the water column.

The formula we have worked out is saying exactly that, the pressure will depend on the height independent of the surface area.

What happens if the tank has a sloped bottom, then p would become a linear function of x, the horizontal position of each point on the sloped bottom.

We are not interested in sloped bottoms or even tanks with odd rectangular shapes. We are establishing a relationship of pressure p vs. a theoretical column height h, when we use static head or even friction head we can always translate that back to a pressure that would be generated at the bottom of a theoretical flat bottom tank.