MICRO-HYDRO INSTALLATION SIZING (CROSS-FLOW TURBINE)

This article is intended to help you build your own cross-flow turbine, also known as a Mitchell-Banki turbine. Mitchell is the original inventor of the turbine around 1900. Banki took up this design and explained its theory of operation in 1916. He claimed that the turbine would be more than 86% efficient. Tests on the cross-flow design were done in 1948 by Mockmore and Merryfield and the best efficiency they were able attain was 68% on a scaled down laboratory model. The results of the experiments were produced in this document titled the Banki Water Turbine by C.A Mockmore & Fred Merryfield, Bulletin Series No.25, Feb. 1949: banki_scan.pdf

Image courtesy of the magazine Sentiers Chasses et Pêches, Juin 1998

The low efficiency that Mockmore and Merryfield achieved may be due in part to the nozzle design; the Banki nozzle was close coupled to the turbine such that the nozzle outlet pressure may have been higher than atmospheric, as compared to the Mockmore and Merryfield design that came in at atmospheric pressure. The Ossberger company in Germany manufactures a cross-flow turbine that they claim is more than 80% efficient. Their nozzle is also close-coupled and the water enters many turbine blades perhaps being responsible for the higher efficiency.

You can visit their web site here:

https://ossberger.de/en/

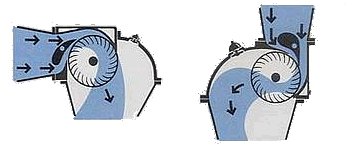
source of image:https://ossberger.de/en/

Figure 2. Ossberger cross-flow turbine.

Lately, I have come across a paper by W.W. Durgin and W.K. Fay titled "Some fluid characteristics of a cross-flow type hydraulic turbine". You can download this paper here: Banki_revisited.pdf

The web site where I discovered this paper is: french river land, a great site with a wealth of information on turbines. This paper shows that the cross-flow turbine can be unstable at certain flow rates and that cross-flow through the turbine does not always occur. The maximum efficiency attained by them was 61%. Even at 61% efficiency the cross-flow design is well worth considering. It must be remembered that the Pelton design starts off with a 50% penalty, that is assuming its design is perfect, it can only extract 50% of the energy from the water due to the fact the turbine wheel can only turn at half the speed of the incoming water jet. Then if you add the losses that occur in transferring power from the water jet to the wheel you come up with an efficiency that is less than 50%. The other reason to consider it is easier to build than to the Pelton.

Dimensions and power extraction capacity of the cross-flow turbine

A cross-flow turbine is a type of turbine that is suitable for low head high flow applications. This is probably a more frequent application than the high head low flow application for which a Pelton turbine is designed. Also a homeowner can more easily build a cross-flow turbine because the turbine blades are a simple shape compared to the complex buckets of the Pelton turbine, however you can buy a Pelton wheel only.

How much flow is available? This is the first item to consider. It is beyond the purview of this article to explain how to determine this but I think that most people will be able to determine whether it is suitable to tap their water source with a 2", 6," or 10" diameter pipe. This web site will give you some ideas as to how to go about it:

Canyon Hydro

This article will be based on the information provided in the C.A Mockmore & Fred Merryfield, Bulletin Series No.25 document that provides detail information on how to size and fabricate the different parts of the turbine.

The remarkable thing about this design is that the water jet enters the turbine tangentially, goes through the blades of a simple circular section, crosses the inside of the turbine and impacts the blades on the other side at an angle that allows more power to be extracted from the water jet.

Here is a nice image of the turbine which I borrowed from Joe Cole's website for which I am grateful and will ask for his permission to use when I manage to reach him.

Figure 2. Cross-flow turbine.

The following image shows the passage of the water jet through the turbine. The centerline of the water jet is shown as the dashed red line.

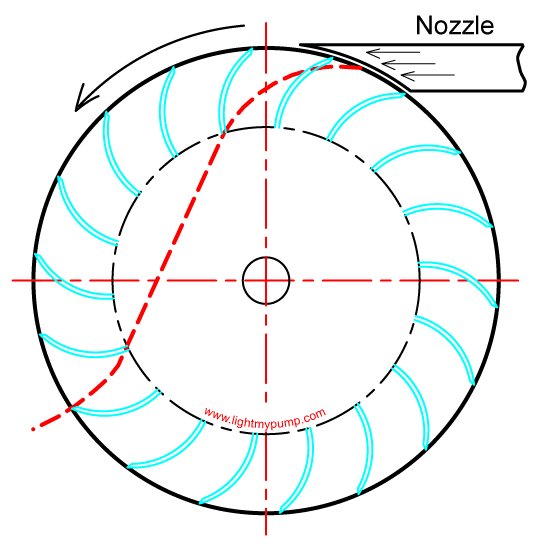
Figure 3. Water flow through the cross-flow turbine.

The water strikes the turbine blade rotating the whole turbine wheel. This rotation moves the water jet forward until it has passed over the blade and fallen through the center of the turbine. It has been calculated that 72% of the water jet's power is extracted at this point. The water jet then reaches the inner edge of the turbine blades where the remaining 28% of the water jet's power.

Before we get into the details as to how to size your turbine and how to determine the power available from the water jet, there are certain geometrical constants that make a cross-flow turbine what it is and thereby ensure that you get close to it's highest possible efficiency. These features are shown in Figure 4.

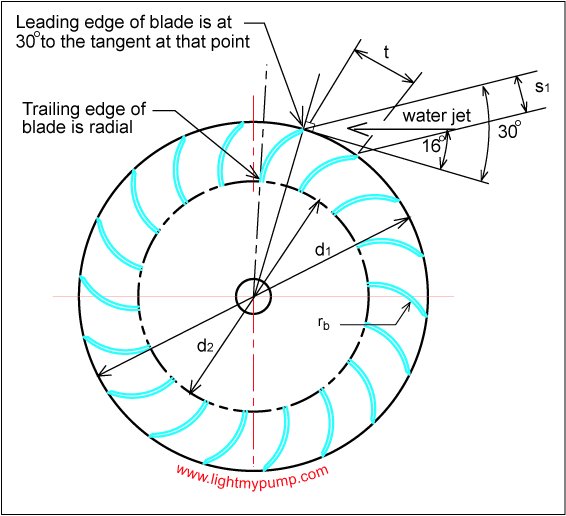
Figure 4. Critical geometry of the cross-flow turbine.

The water jet angle to the blades should be 16 degrees with respect to the tangent at the point of contact (more about the width of the water jet later). The leading edge of the blade should be at 30 degrees to the tangent at the point of contact. The trailing edge of the blade is radial, that is all the trailing edges point directly to the center. The blades are made from circular sections of radius rb and the spacing t will be calculated depending on the overall diameter d₁ of the turbine.

Most of the construction dimensions of the Banki turbine can be established using the outside diameter d₁ (see Figure 4) and the relationships given in the Mockmore & Merryfield document that I will be using here. I am merely extracting from that document the relevant formulas that are used for sizing the turbine.

We will start our turbine sizing using an outside diameter of 12". I will be using the Imperial system of measurements.

d₂/d₁ = 0.66 therefore d₂ = 7.92"

The radius of the blade r_b is given by:

r_b = 0.326 x d₁/2 = 1.96"

The spacing of the blades t is given by

s₁ = k x d₁ with k = 0.09 therefore s₁ = 1.08"

and t = s₁/sin β₁ than where β₁= 30

t = 1.08/ sin 30 = 2.16"