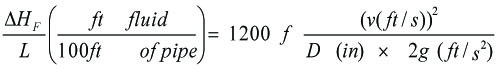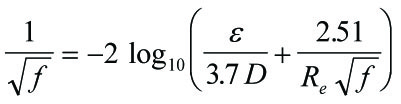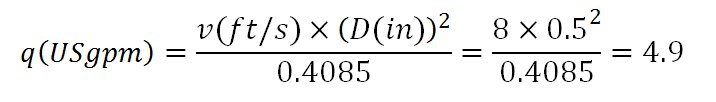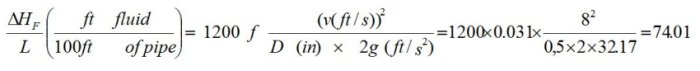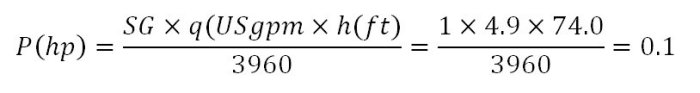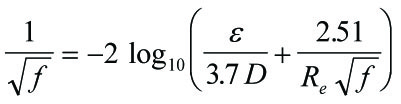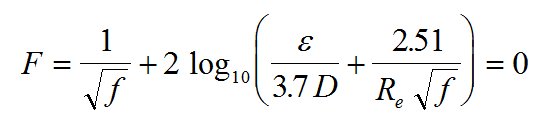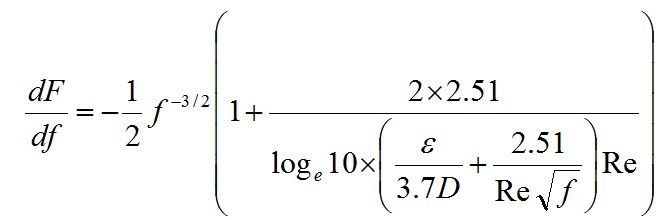Friction - small vs large pipes
Jacques Chaurette
May 2016
download in pdf format
It is an interesting fact that friction is higher in small pipes than larger pipes for the same velocity of flow and the same length.
Friction is determined by the Darcy-Weisbach equation which in turn relies on the friction parameter given from the Colebrook equation.
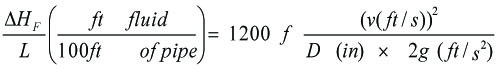 Figure 1 Darcy-Weisbach equation for calulating the friction factor.
Figure 1 Darcy-Weisbach equation for calulating the friction factor.
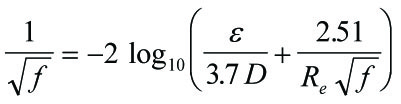 Figure 2 Colebrook equation for calulting the friction parameter.
Figure 2 Colebrook equation for calulting the friction parameter.
In the latter equation the relative roughness ε/D is a major component of friction. This number is large for small tubes which makes friction higher.
The following graph shows the variation in friction factor for typical pump discharge velocities between 8-13 ft/s and pipes ranging
in size from 0.5 to 12 inches. For these calculations I have used the absolute roughness for steel (0.00015 ft) which is a very common
material. Small tubes could be in polyethylene or some clear soft plastic material both of which would have a similar roughness or lower than steel.
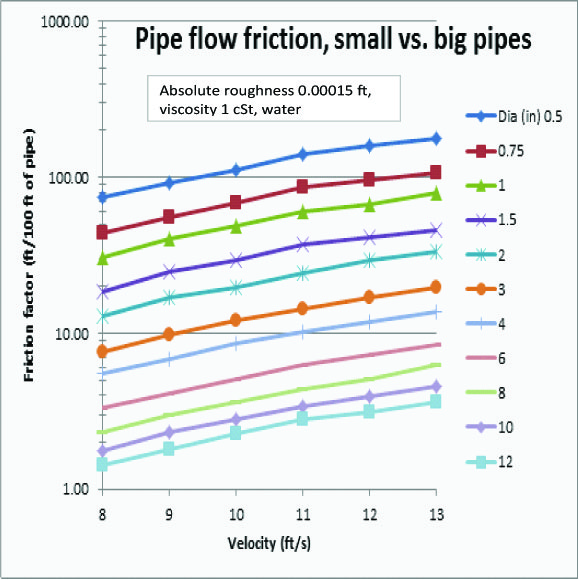 Figure 3 The friction factor vs velocity for different velocities.
Figure 3 The friction factor vs velocity for different velocities.
As we can see, the friction factor is low for large pipes and high for small ones. It is as much as 50 times higher for the velocity range and pipe sizes considered.
Thankfully, since most projects that use small tubes have generally short distances to cover, the higher friction does not become a problem. The
other factor is that most small projects use pumps that produce relatively low head that will generate low velocities therefore lower friction.
What about power? If we compare the friction power or power required to overcome friction we find that the larger pipes will require more power because of
the higher flow rates as expected.
 Figure 4 The friction power vs velocity for different velocities.
Calculations
Figure 4 The friction power vs velocity for different velocities.
Calculations
The friction parameter was determined by using the Moody diagram (shown below). It is possible to calculate the friction parameter directly by the
Colebrook equation by using the Newton-Raphson iteration technique which is in my book and I have included here for convenience. The rest of the
calculations are straight forward and here is an example:
Velocity is given
The flow rate for power calculation is:
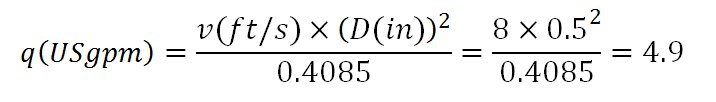 The relative roughness is:
The relative roughness is:
 The friction factor from Darcy-Weisbach:
The friction factor from Darcy-Weisbach:
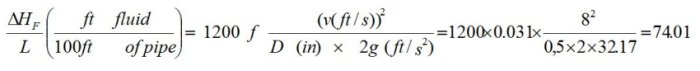 Friction:
Friction:
 Friction power:
Friction power:
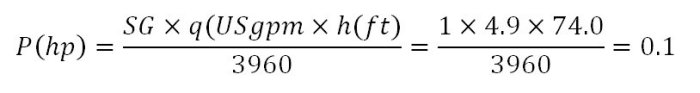
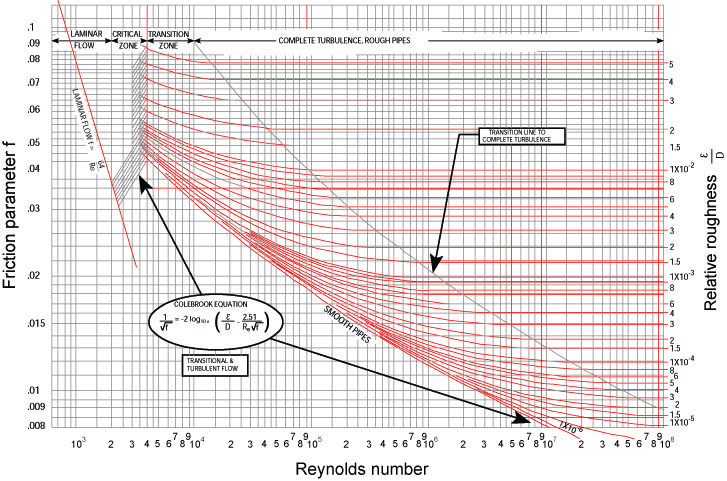
The Newton-Raphson Iteration Technique
Since the value for f in the Colebrook equation cannot be explicitly extracted from the equation, a numerical method is required to
find the solution. Like all numerical methods, we first assume a value for f, and then, in successive calculations, bring the
original assumption closer to the true value. Depending on the technique used, this can be a long or slow process.
The Newton-Raphson method has the advantage of converging very rapidly to a precise solution. Normally only two or
three iterations are required.
The Colebrook equation is:
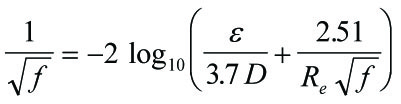
The technique can be summarized as follows:
1. Re-write the Colebrook equation as:
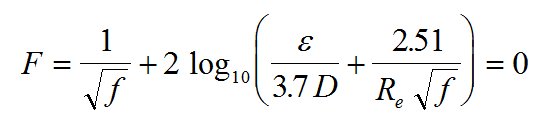
2. Take the derivative of the function F with respect to f:
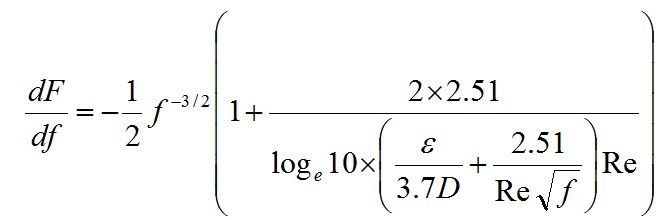
3. Give a trial value to f. The function F will have a residue (a non-zero value). This residue (RES) will tend towards zero very
rapidly if we use the derivative of F in the calculation of the residue.

For n = 0 assume a value for f
0, calculate RES and then f
1, repeat the process until RES is sufficiently small (for example RES < 1 x l0
-6).
The Newton-Raphson iteration technique is a method that converges very rapidly to a solution. You need to provide a seed value for f
n-1 to start the iteration
and an acceptable error RES which you can make very small.
You can find an example of the solution at this link:
www.pumpfundamentals.com/solving_colebrook.htm
which makes use of an Excel spreadsheet and the Goal/Seek function.
Copyright 2016, PumpFundamentals.com